7.1 Verwandtschaftsgrad berechnen
Der Verwandtschaftskoeffizient gibt die Wahrscheinlichkeit an, mit der ein Lebewesen aufgrund seiner Abstammung von seinen Vorfahren ein bestimmtes Allel besitzt. Graphisch lassen sich die Verwandtschaftsverhältnisse wie in Abb. 7.1 darstellen.
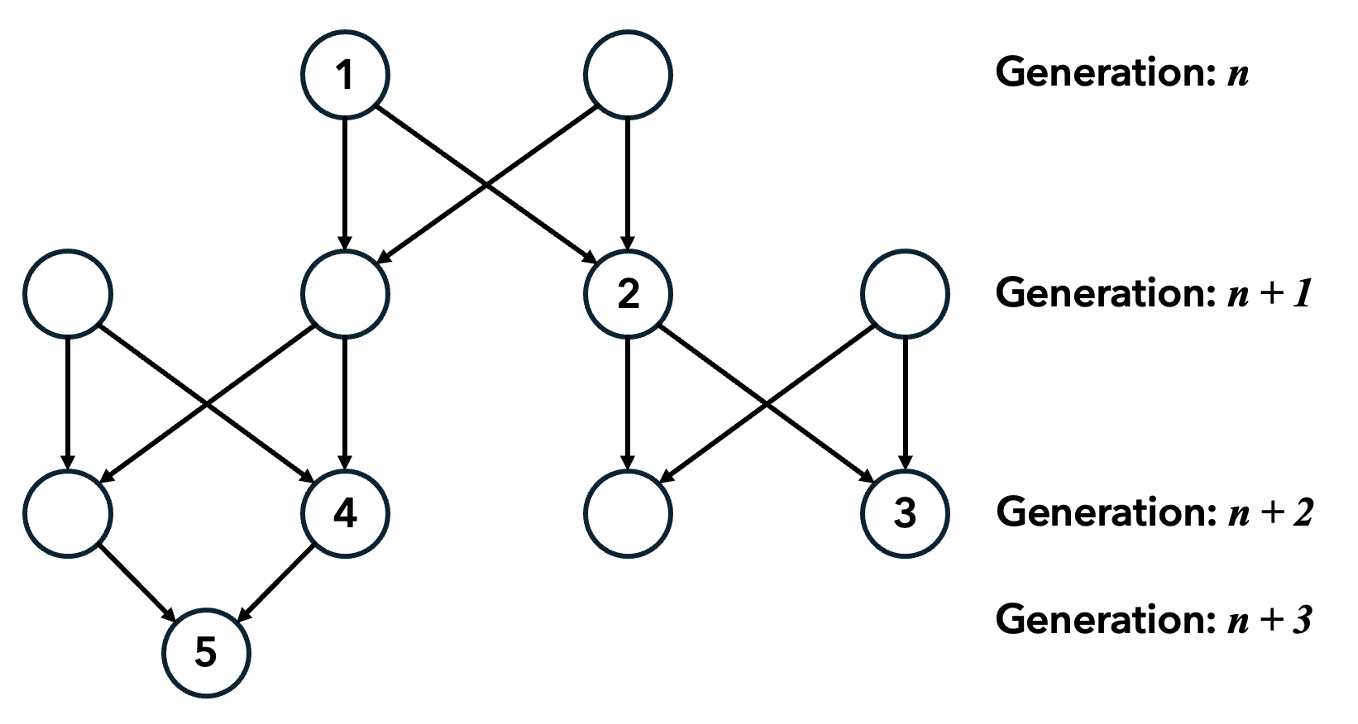
Abbildung 7.1: Verwandtschaftsverhältnisse über vier Generationen.
Kreise entsprechen dabei einzelnen Individuen und Pfeile geben die Abstammungsrichtung an. Da der Entstehung der Gameten eine Meiose (Reifeteilung) vorangeht, ist die Wahrscheinlichkeit für ein Allel, in eines der Kinder zu kommen, 0.5 oder 50%. Wenn das Allel über mehrere Generationen \(n\) weitergegeben wird, so halbiert sich die Wahrscheinlichkeit für jede Generation.
Der Verwandtschaftskoeffizient lässt sich demnach wie folgt berechnen: Die Wahrscheinlichkeit eines Allels aufgrund von Verwandtschaftsverhältnissen in zwei Individuen vorhanden zu sein, ist \(r=(0.5)^n\). Gibt es mehrere Wege, von einem Individuum zum anderen zu kommen, summieren sich diese Wahrscheinlichkeiten.
Beispiel: \(r\) für Individuen 1 und 3: Nur 1 Weg ist möglich und 2 Schritte sind nötig. Daher ist \(r=(0.5)^2=0.25\). Die Wahrscheinlichkeit, dass der Enkel ein bestimmtes Allel des Grossvaters besitzt, ist also 25%.
○ Aufgabe 1. Erklären Sie die Formel \(r=(0.5)^n\) in eigenen Worten.
◑ Aufgabe 2. Berechnen Sie \(r\) für Individuen 2 und 4, sowie Individuen 3 und 4.