7.4 Der Verwandtschaftskoeffizient – eine zweite Erweiterung
Wie wir im vorherigen Kapitel gesehen haben, gilt diese Formel für diploide Organismen. Deshalb ist auch der multiplizierte Faktor 0.5. Nur die Hälfte des Genoms wird an die nächste Generation vererbt. Anders sieht es allerdings aus, wenn wir nicht mehr diploide, sondern haploide Organismen betrachten.
Im einfachsten Fall stammt also das haploide Kind von einem haploiden Elternteil ab. welches ebenfalls von einem haploiden Elternteil abstammt. Da in diesem Fall keine Meiose stattfindet, erben alle Kinder das gleiche Erbgut wie die jeweiligen Eltern, welche ebenfalls das komplette Genom ihrer Eltern geerbt haben. Man hat also eine Klonierung haploider Organismen.
Die Verwandtschaftsverhältnisse sind intuitiv klar: man hat einen Verwandtschaftsgrad von 100%, da die Kindsgeneration die exakt gleichen Gene tragen. Mathematisch kann man hingegen die Formeln nicht mehr anwenden. Um eine allgemeingültige Formel zu erhalten, müssen wir daher Formel 7.2 (als allgemeinere Form der Formel 7.1) entsprechend anpassen:
\(r = \sum_{i=1}^{k} P^{n_i} \tag{7.3}\)
mit \(P\) als den Kehrwert des Ploidiegrads (Anzahl vorhandener Chromosomensätze) der zu untersuchenden Individuen von einer bestimmten Abstammung.
Für den Verwandtschaftsgrad im haploiden Beispiel ergibt sich folglich vom Grosselternteil zu Elternteil \(r=1^1=1\), da \(P=1\) und \(n=1\) Generation; für den Verwandtschaftsgrad von Elternteil zu Enkelkind ergibt sich \(r=1^2=1\) mit \(n =2\) Generationsschritte. Dass das Resultat das gleiche ist, macht ebenfalls Sinn, da es sich um Klone handelt.
Die ursprünglich eingeführte Formel 7.2 erlaubt daher zwar in simplen Beispielen den Verwandtschaftsgrad zwischen zwei Individuen zu berechnen, stösst allerdings ziemlich schnell an seine Grenzen, wenn auf mehr als nur eine Art die Verwandtschaft erklärt werden kann oder wenn die Individuen nicht diploid sind. Die allgemeingültigere Formel 7.3 für den Verwandtschaftsgrad (oder Verwandtschaftskoeffizienten) muss deshalb angepasst werden; mit \(r\) als Verwandtschaftskoeffizienten, \(k\) als maximale Anzahl Wege, um Verwandtschaft zu erklären, \(n_i\) als Anzahl Generationsschritte eines Weges \(i\), und \(P\) als den Kehrwert des Ploidiegrades, mit \(P=1\) bei haploiden und \(P=0.5\) bei diploiden Organismen.
Mithilfe der erarbeiteten Formeln können nun die Verwandtschaftsverhältnisse auch in komplexeren Systemen wie dem Bienenstock betrachtet werden. Im Bienenstock gibt es folgende Bienen:
Königin: diploid, legt unbefruchtete und befruchtete Eier
Arbeiterinnen: diploid, aus befruchteten Eiern der Königin
Drohnen: männliche Bienen, haploid, aus unbefruchteten Eiern der Königin
Was in allen Tieren gleich ist, ist, dass die Königin durch Meiose haploide Eier produziert. Worin sich allerdings die Honigbiene von vielen anderen Tieren unterscheidet, ist, dass sie entweder diese Eier unbefruchtet legen kann, woraus schlussendlich die Drohnen schlüpfen, oder befruchtet legen kann, woraus Arbeiterinnen schlüpfen.
◑ Aufgabe 6. Berechnen Sie den Verwandtschaftsgrad einer Arbeiterin und einer Drohne mit der Königin. Nehmen Sie sich dazu die Abbildung 7.3 zu Hilfe.
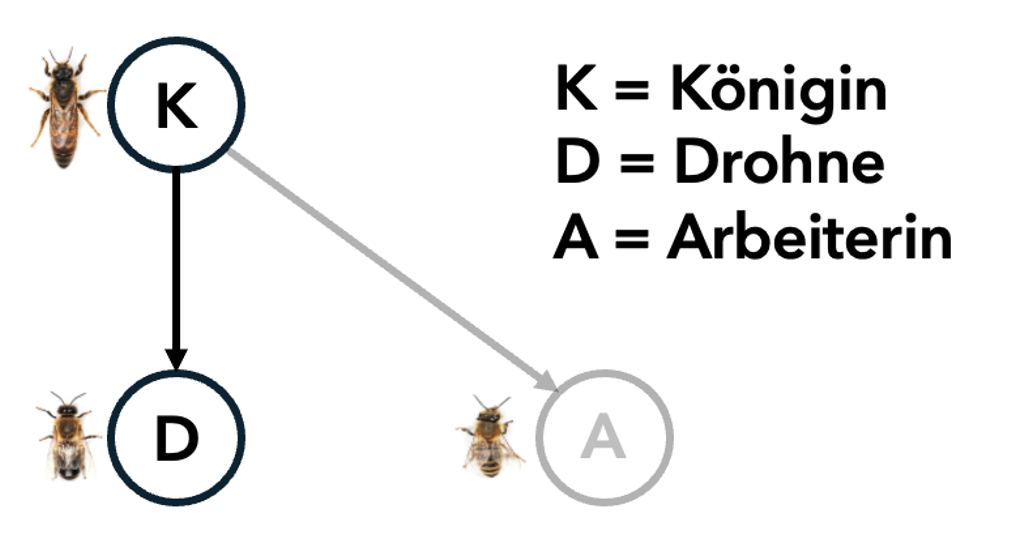
Abbildung 7.3: Abstammungsverhältnisse im Bienenstock.
● Aufgabe 7. Vor welchem Problem stehen wir, wenn wir herausfinden möchten, wie hoch der Verwandtschaftsgrad zwischen einer Drohne und einer Arbeiterin mit der gleichen Königin als Mutter ist?