7.5 Der Verwandtschaftskoeffizient – eine dritte und letzte Erweiterung
Um der Situation gerecht zu werden, dass nicht alle Generationswege \(n_i\) den gleichen Ploidiegrad \(P\) haben müssen, muss also unsere Formel entsprechend angepasst werden. Aus Beispiel der Drohnen und Arbeiterinnen derselben Mutter kann man schliessen, dass die Drohnen zwar mit der Mutter einen Verwandtschaftsgrad von \(r=1\) haben und die Arbeiterinnen mit der Mutter \(r=0.5\). Wenn in beiden Schritten diploide Individuen vorkämen, dann ginge die Formel mit \(r\) als das Multiplikationsprodukt der beiden Wahrscheinlichkeiten auf (\(r=0.5*0.5=(0.5)^2\)).
Da wir aber nun einen Ploidiewechsel in den zwei Generationsschritten (n=2) haben, entsteht in unserer Formel ein Widerspruch \(r=1*0.5 ≠(0.5)^n=(0.5)^2\). Viel eher müsste man also das Produkt der Einzelwahrscheinlichkeiten (d.h. der Ploidiegrade) der einzelnen Schritte betrachten. Die angepasste Formel lautete daher:
\(r = \sum_{i=1}^{k} \left( \prod_{j=1}^{n} P_{i,j} \right) \tag{7.4}\)
mit
\(r\) als Verwandtschaftskoeffizienten
\(k\) als maximale Anzahl Wege \(i\), um Verwandtschaft zu erklären
\(n\) als maximale Anzahl Generationen aus \(j\) Generationsschritten
\(P_(i,j)\) als Ploidiegrad des Schrittes j auf dem Weg \(i\) mit \(P_(i,j)=1\) bei Schritten haploider Organismen und \(P_{(i,j)}=0.5\) bei Schritten von diploiden Organismen.
Die Überlegungen aus dem vorherigen Kapitel bezüglich der Anzahl Wege, um die Verwandtschaft zwischen Arbeiterin und Drohne zu zeigen (1 möglicher Weg mit indirekter Verwandtschaft, \(k=1\)), und der Anzahl benötigter Generationsschritte (\(n=2\)) sind immer noch valide. Der Ploidiegrad muss allerdings für \(j=1\) von der Drohne zur Mutter und \(j=2\) von der Mutter zur Arbeiterin unabhängig voneinander bestimmt werden. Daher folgt: \(r=P_1*P_2=1*0.5=0.5\)
Aufgrund dessen, dass die Drohnen einen Verwandtschaftsgrad von 100% mit der Mutter aufweisen, ist also der Verwandtschaftsgrad zu den Schwestern (Arbeiterinnen), unabhängig von deren Vater, 50%.
Der letzte Vergleich, der jetzt noch fehlt, um die Tabelle im Kapitel 5.2 zu vervollständigen, ist derjenige zwischen Arbeiterinnen mit gleichen und unterschiedlichen Vätern. Dies werden wir zusammen an Beispielen erarbeiten. Versuchen Sie dabei, die Schritte genau nachzuvollziehen.
Verwandtschaftsgrad zwischen zwei Arbeiterinnen.
Da der Vater haploid ist und seine Spermien daher keine Meiose durchlaufen, erben alle Nachkommen des Vaters die gleichen Gene. Väterlicherseits haben Arbeiterinnen also einen Verwandtschaftsgrad von 100% (\(r=1^1=1\) mit \(P= n=k=1\)). Der Verwandtschaftsgrad mütterlicherseits haben wir bereits im vorherigen Kapitel berechnet.
Um nun den Verwandtschaftsgrad zwischen zwei Arbeiterinnen zu berechnen, müssen wir zwei Fälle unterscheiden: einmal mit gleichem Vater und einmal mit anderem Vater. Je nachdem, welchen Fall wir haben, haben wir eine andere Anzahl Wege, um die Verwandtschaft zu erklären.
Beispiel 1: Arbeiterinnen mit unterschiedlichem Vater
Wenn die Arbeiterinnen die gleiche Mutter, aber unterschiedliche Väter haben, dann gibt es nur den Weg über die Mutter, um die Verwandtschaftsverhältnisse zu erklären (\(k=1\)) (Abb. 7.4A).
Der Verwandtschaftsgrad lässt sich also wie folgt berechnen: Es gibt hierbei einen Generationenwechsel mit \(n=2\) Generationenschritten. Wir haben keinen Ploidiewechsel, da beide Schritte über die Mutter zu den Arbeiterinnen geben, wobei alle diploid sind (\(P_j=0.5\)). Es folgt also (ohne die Summenformel, da \(k=1\)): \(r = \prod_{j=1}^{2} P_j = \prod_{j=1}^{2} 0.5 = 0.5^2 = 0.25\)
Dadurch ergibt sich, dass Arbeiterinnenschwestern mit unterschiedlichem Vater einen Verwandtschaftsgrad von 25% aufweisen. Sie sind also Halbschwestern. Diese Berechnung bestätigt die intuitive Beobachtung von Halbschwestern bei diploiden Organismen.
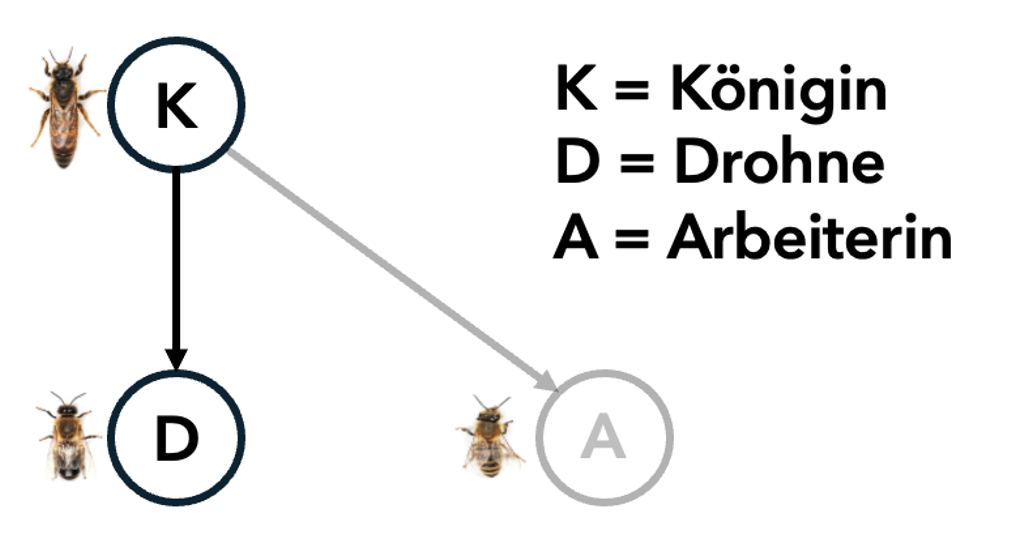
Abbildung 7.4: Abstammungsverhältnisse der Arbeiterinnen im Bienenstock im Vergleich mit dem Vater.
Beispiel 2: Arbeiterinnen mit gleichem Vater
Wenn der Vater der Arbeiterinnen der gleiche ist, dann gibt es zwei Wege, um die Verwandtschaft zu erklären, nämlich einen über die Mutter (Königin) und einen über den Vater. Daher folgt \(k=2\) (Abb. 7.4B). Zudem haben wir über den Weg beim Vater einen Ploidiewechsel.
◑ Aufgabe 8. Berechnen Sie mithilfe der Formel 7.4, welchen Verwandtschaftsgrad zwei Arbeiterinnen mit gleichem Vater aufweisen.
◑ Aufgabe 9. Vergleichen Sie den Verwandtschaftsgrad zwischen Schwestern mit dem Verwandtschaftsgrad mit eigenen Kindern von Arbeiterinnen. Was fällt Ihnen diesbezüglich auf?
● Aufgabe 10. Nur jene Bienenlarven, die dauerhaft mit Gelee Royal, eine nährstoffreiche Substanz, gefüttert werden, können sich zu neuen Königinnen entwickeln. Deren Schwesterlarven entwickeln sich zu Arbeiterinnen. Welche Konsequenz hat dies auf das Verhältnis zwischen Arbeiterin und Königin in der nächsten Generation der Bienen im Bienenstock?
● Aufgabe 11. Welche Auswirkungen könnten diese Verwandtschaftsverhältnisse auf das Verhalten der Bienen im Kontext der biologischen Fitness haben?